Skip to contents

Evaluate \(F_j\) and Recovery the Trajectory for a Single Variable

Source: R/evaluate_Fj.R
evaluate_Fj.Rd

Evaluates the derivative function \(F_j\) of a single variable on the integration grid tt and recovers the trajectory by numerical integration, given estimates of \(b_j\), \(c_j\), and \(\theta_j\).

Usage

evaluate_Fj(
  bj,
  cj,
  interaction_term,
  kernel,
  kernel_params,
  kk_array = NULL,
  obs_time,
  theta_j,
  tt,
  Yj,
  yy_smth
)

Arguments

bj

A numeric scalar, giving the estimated \(b_j\) from Kernel ODE (i.e., res_bj[j]).

cj

A numeric vector of length n, giving the estimated \(c_j\) from Kernel ODE (i.e., res_cj[,j]).

interaction_term

A logical value specifying whether to include interaction effects in the model.

kernel

Kernel function to use.

kernel_params

A list of length p, where each element is a named list of parameters for a specific variable (e.g., list(bandwidth = 1) for Gaussian kernel). If the list has length 1, the same parameter set is used for all variables. This is typically the output of auto_select_kernel_params().

kk_array

Optional precomputed kernel array on tt. An array of dimension (len, len, p) when interaction_term = FALSE, or (len, len, p^2) when interaction_term = TRUE, where len = length(tt). Providing kk_array enables reuse across variables and can greatly reduce computation.

obs_time

A numeric vector of length n representing observation time points.

theta_j

A numeric vector of length p (if interaction = FALSE) or p^2 (if interaction = TRUE), giving the estimated \(\theta_j\) coefficients for variable \(j\) from Kernel ODE (i.e., res_theta[,j]).

tt

A numeric vector representing a finer time grid used for evaluating the smoothed trajectories and their derivatives.

Yj

A numeric vector of length n, giving the observed trajectory for variable \(j\) (i.e., Y[, j]).

yy_smth

Numeric matrix of dimension (len, p); smoothed trajectories evaluated on tt (i.e., output of kernelODE_step1()).

Value

A list with components:

theta_j0

A numeric scalar giving estimated initial condition for variable \(j\).

Fj_est

A numeric vector (length len) giving the evaluated \(F_j\) on tt.

yy_est

A numeric vector (length len) giving the recovered trajectory on tt.

TV_est

A numeric scalar giving the total variation \(\int |F_j(t)| \, dt\) approximated on tt.

tt

Same as the input tt, the grid on which \(F_j\) and the trajectory is evaluated.

Details

Given \(b_j\), \(c_j\), and \(\theta_j\), the function constructs the kernel-weighted integral operator on the grid tt to evaluate \(F_j\), estimates the initial condition \(\theta_{j0}\), then recovers the trajectory via cumulative summation on tt (first-order approximation). When provided, kk_array is reused to avoid recomputing kernel blocks.

See also

kernelODE_step1(), kernelODE_step2(), assess_recov_traj()

Examples

set.seed(1)
obs_time <- seq(0, 1, length.out = 10)
Y <- cbind(sin(2 * pi * obs_time), cos(4 * pi * obs_time)) + 0.1 * matrix(rnorm(20), 10, 2)  # each col is a variable
tt <- seq(0, 1, length.out = 100)
res_step1 <- kernelODE_step1(Y = Y, obs_time = obs_time, tt = tt)

kernel <- "gaussian"
kernel_params <- auto_select_kernel_params(kernel = kernel, Y = Y)
res_step2 <- kernelODE_step2(Y = Y, obs_time = obs_time, yy_smth = res_step1$yy_smth, tt = tt, kernel = kernel, kernel_params = kernel_params)

j <- 1  # evaluate Fj for the first variable
res_eval <- evaluate_Fj(bj = res_step2$res_bj[j],
                        cj = res_step2$res_cj[,j],
                        interaction_term = FALSE,
                        kernel = kernel,
                        kernel_params = kernel_params,
                        obs_time = obs_time,
                        theta_j = res_step2$res_theta[,j],
                        tt = tt,
                        Yj = Y[,j],
                        yy_smth = res_step1$yy_smth)
yy_j_est <- res_eval$yy_est

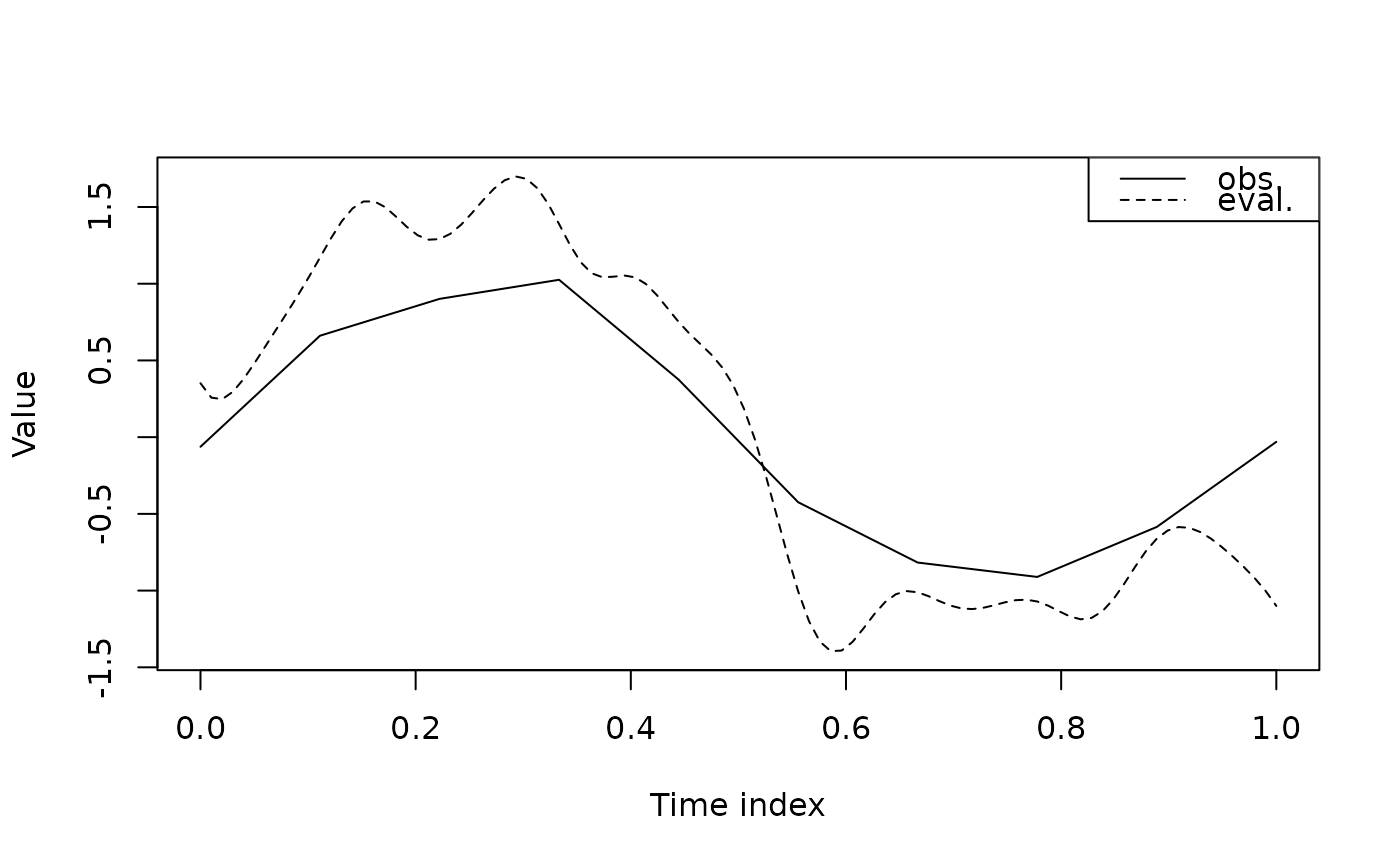
# plot the evaluated traj
plot(NA, type = "n",
     xlab = "Time index", ylab = "Value",
     xlim = c(0,1), ylim = range(c(yy_j_est, Y[,j]), na.rm = TRUE))
lines(obs_time, Y[,j], lty = 1)
lines(tt, yy_j_est, lty = 2)
legend("topright",
       legend = c("obs.", "eval."),
       lty = c(1,2),
       col = "black")